聊一聊 Transformer
1. 引言
Transformer (Vaswani et al., 2017) 在 AI 的发展中称得上是一种划时代的技术。目前,几乎所有大语言模型 (Large Language Model,LLM) 的模型架构均是在 Transformer 架构的基础上演变而来。另外,现代 AI 推理引擎的核心优化目标,以及专用 AI 加速硬件的设计理念,都会涉及 Transformer 的结构特性。因此,想要走进当下的 AI 领域,Transformer 是绕不开的。
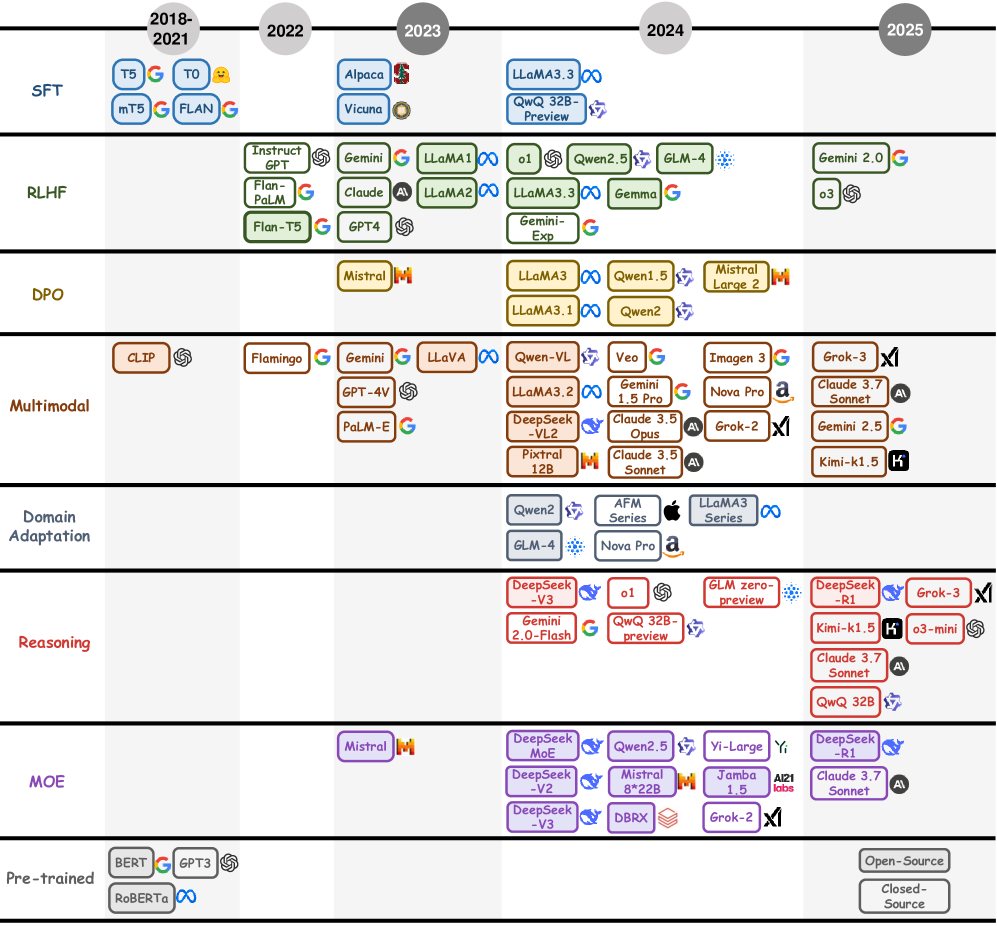
这篇文章希望能为大家展示 Transformer 的前因与后果,不局限于 Transformer 的技术原理,而是展示这一段技术演变的历史过程,最大的目标是能让大家感受到一些 AI 之美。
本次分享将按以下脉络展开:
- 前置基础:文本是如何转化为可计算的数学表示的?
- 历史背景:Transformer 诞生的历史背景,它旨在解决哪些核心问题?
- 技术原理:Transformer 技术原理的通俗解释。
- 后续演进:Transformer 架构在后续 LLM 中的应用,Transformer 架构在 LLM 中发生了哪些关键变化?
2. 文字的数学表示
关键问题: LLM 本质上是基于概率的数学建模系统,但自然语言符号本身不具备可计算性,那计算机是如何对文字进行计算的呢?是如何将文字转化为可计算的数据表示?
Transformer 是一种广泛应用于自然语言处理(Natural Language Processing,NLP)领域的 Seq2Seq 模型。在深入理解 Transformer 之前,首先需要了解 NLP 任务中如何将文本转换为可计算的数学表示,这一步骤是所有 NLP 模型的基础和关键,也是迈入 NLP 领域的起点。
注:
Seq2Seq 模型:在 NLP 中,Seq2Seq(Sequence-to-Sequence)泛指一类模型,这类模型的核心思想是将输入序列映射为输出序列,两者长度可以不同。
在 LLM 中,通过分词(Tokenization)与词嵌入(Word Embedding)两个步骤对文本进行预处理,将文本转化为可计算的数学表示。
- 分词:将一段文本分割为一系列词语单元,这里的词语单元就是我们经常看到的 token。
- 词嵌入:将通过分词得到的一系列 token 逐个转化为数值向量,每个 token 会具有一个唯一 ID(比如:1、2、3 等),词嵌入会将每个 token 的 ID 转化为一个数值向量。
2.1 分词
可能第一印象会觉得分词在 LLM 中是无关紧要的,其实不然,LLM 输入与输出的基本单位是 token,具体有哪些 token,这是由分词器的词表决定的?也就是说 LLM 的语言表征能力是深度依赖分词器的,如果底层分词器词表质量较差,上层模型的结构设计得不论多优良都是不行的。
分词(Tokenization)的核心任务是将连续的自然语言文本切分成一系列词语单元(token)。执行分词这个动作的工具被称为分词器(Tokenizer)。例如,对于输入文本“今天天气怎么样?”,分词器将其分解为 token 序列 [“今天”, “天气”, “怎么样”, “?”]。分词器需要预先根据训练语料构建词表,再基于词表对输入文本进行分词。
那什么样的分词器是好的呢?最直观的想法是,我们希望词表要能很好地保留语义特征,比如“苹果”这个词,希望其在分词结果中被保留为一个完整的词语单元,而不是被切分成“苹“和”果”两个词语单元,切分的粒度太粗或太细都是不好的。然后,要能很好地适应各种类型的语言和文字符号,比如数值、Emoji 等。另外,要有较好的工程效率,能够较快地对文本完成分词与逆分词,能够为下游训推任务减轻负担。
如果平常大家有使用 Hugging Face 下载过 LLM 模型文件,会发现每个 LLM 的模型仓库里基本都会有一个tokenizer.json文件,这个文件存储了其 tokenizer 完整的配置信息,当然也包括词表数据。
2.1.1 基于规则的分词
早期的词表构建方法通常是基于各种规则对训练语料进行分割,比如空格、标点及一些语法特征等,下面的例子来自 Summary of the tokenizers。
Don't you love Transformer? We sure do.
最简单的分词是基于空格对语料进行切分,比如上面这段叙述,将被切分为
"Don't", "you", "love", "Transformer?", "We", "sure", "do."
Don't,Transformer? 与 do. 的切分结果还不够好,可以再进一步基于标点进行切分,这一次得到
"Don", "'", "t", "you", "love", "Transformer", "?", "We", "sure", "do", "."
但对于 Don't 的分词结果 "Don", "'", "t" 还不够理想,希望通过特定语法规则将其分解为 "Do", "n't",其中 n't 为 Do 增加否定之意,这里已经有了子词的意味,再举几个例子,比如,将 apples 分解为 "apple", "s",将 doing 分解为 "do", "ing"。
"Do", "n't", "you", "love", "Transformer", "?", "We", "sure", "do", "."
根据分词的粒度,可以将基于规则的词表构建方法大概分为三类:
- 基于字母的分词,这种方法的词表尺寸最少(分割粒度过细),但会增大下游任务的复杂度,需要花费更多时间来学习如何基于词表来表征当前的语言范畴,有一个比较形象的例子,其实我们可以用红绿蓝表示任何一种颜色(RGB 值),类似于直接使用字母进行分词,但在日常生活中,比如挑选口红,我们不会使用 RGB 值,这样会很不方便,而是使用一些约定俗成的色号;
- 基于单词的分词,这种方法的结果数量过大(分割粒度过粗),会降低模型的泛化性;
- 基于子词的分词,这是一种比较折中的方案,将文本中的单词分解为基本单词和附加部分,附加部分为基本单词添加额外含义,比如否定、复数、时态等。
2.1.2 基于统计的分词
随着 NLP 任务中语料规模的增大,越来越倾向于使用基于统计的方法来构建词表。
2.1.2.1 WordPiece
在 WordPiece (Wu et al., 2016) 中,对于训练语料,先基于最基本的词语单元构成一个初始词表,比如对于英文语料,可能是英文字母和常见的标点符号;对于中文,可能是基础汉字和常见的标点符号;对于现代大语言模型,可能就是 256 种可能的字节。然后,基于初始词表,经过一定轮数的迭代形成最终的词表,迭代的终止条件一般是词表的大小达到预定的要求,每轮迭代会选出一个新的词语单元添加进词表,选取方法如下公式所示:
\[\begin{equation} \arg \max_{x, y \in D} \frac{ {\rm count} (x y)}{ {\rm count} (x) \times {\rm count} (y)} \end{equation}\]其中,${\rm count}(\cdot)$ 表示词语单元在语料中的出现次数,$D$ 表示当前的词表,$x$ 与 $y$ 表示当前词表中任意两个词语单元。这个公式的思路就是从当前词表中选取两个词语单元 $x$ 与 $y$ 组合成一个新的词语单元 $x y$,这两个词语单元 $x$ 与 $y$ 要满足,将两者相连作为新的词语单元 $x y$ 在训练语料中的出现次数 ${\rm count} (x y)$ 除以两者各自在训练语料中的出现次数的乘积 ${\rm count} (x) \times {\rm count} (y)$ 的结果最大。
这个思路基于这样一种概率理论,对于事件 $X$ 与事件 $Y$,$\frac{p(X, Y)}{p(X)p(Y)}$ 的值越大,事件 $X$ 与事件 $Y$ 的相关性越强。
2.1.2.2 BPE
Byte Pair Encoding(BPE)(Shibata et al., 1999) 算法和 WordPiece 算法非常相似,只是 BPE 算法是直接选取 ${\rm count} (x y)$ 最大的 $x y$ 作为新的词语单元添加进词表。
\[\begin{equation} \arg \max_{x, y \in D} {\rm count} (x y) \end{equation}\]2.1.2.3 Unigram
Unigram (Kudo, 2018) 算法的思路较复杂一些,WordPiece 算法与 BPE 算法的词表构建是由小到大,而 Unigram 算法是由大到小,Unigram 算法会预先使用某种启发算法,比如 BPE 算法或 WordPiece 算法,生成一个很大的词表,然后进行迭代,每次迭代会从词表中剔除一个词语单元直至词表缩减至预定大小,该词语单元需要满足,对于训练语料是由当前词表构成的似然,它的影响最小的,似然可以写为如下形式:
\[L = - \sum_{i=1}^{N} \log \left( \sum_{j=1}^{K(i)} \prod_{x \in D_{i,j}} p(x) \right)\]其中,假设训练语料可先切分为 $N$ 段,对于第 $i$ 段有 $K(i)$ 种切分方式,对于第 $i$ 段、第 $j$ 种切分方式所用到的词语单元集合记为 $D_{i, j}$,需要剔除的词语单元的选取方法如下所示:
\[\arg \min_{x \in D} L(D) - L(D_{-x})\]其中,$D$ 表示当前词表,$D_{-x}$ 表示 $D$ 去除词语单元 $x$ 得到的新词表。另外,Unigram 算法的工程实现中通常使用 Viterbi 算法进行优化。
2.1.2.4 总结
对于这三种词表构建算法,Unigram 算法最为复杂,它属于 n-gram 语言模型中最简单的一种,它虽然复杂,但有一个好处是,Unigram 算法的分词结果是一个概率分布,tokenizer 可根据分词结果进行采样,它的输出是弹性的,也更为灵活;WordPiece 算法与 BPE 算法的分词结果是唯一的(或者刚性的),Unigram 算法还有一个好处是可以比较方便的对词表进行剪裁。另外,WordPiece 算法与 BPE 算法可以将词表组织为数组形式的 Trie 数据结构以提升分词性能。
SentencePiece 是目前非常流行的分词器,它集成了 Unigram 算法(默认)和 BPE 算法,它将文本视为字符流,无需依赖特定语言的预处理或后处理,对于各种语言都有较好的支持。
目前 LLM(如 DeepSeek V3)普遍采用 Byte-level Byte Pair Encoding(BBPE)算法,该算法在字节级别构建词表,能更好地处理多语言和特殊字符。
2.1.3 文本归一化
在实际应用中,文本归一化(Text Normalization)是构建词表前的关键预处理步骤,目的是将不同形式、书写习惯或字符表示的文本统一为一致的格式,以避免因表面形式的差异导致分词错误。
- 形式统一化:消除书写变体(如全角/半角字符)、拼写差异(如美式/英式英语)和字符编码差异(如 Unicode 组合字符),比如“colour”(英式)与“color”(美式)、Unicode 编码的 NFKC 标准化处理;
- 语义一致性:确保相同语义的文本单元获得相同的向量表示,比如“café”与“cafe”、“I’m”与“I am”;
- 词表效率:通过减少表面形式的多样性,提升词表的空间利用率。
2.2 词嵌入
词嵌入(Word Embedding)的核心任务是将 tokenizer 输出的每个 token 对应的 One-Hot 向量映射为一个稠密向量(Dense Vector)。例如,token“今天”可能被转化为向量 $[1.1, 1.2, 2.0]$。
为什么叫“词嵌入”(Embedding)而不是“向量化”? 这一术语的起源可以追溯到 2013 年 Google AI 提出的 Word2vec (Mikolov et al., 2013) 模型。词嵌入不仅实现了简单的向量化,还蕴含了更深层的设计理念:
- 语义编码:语义相近的词,其向量在空间中的距离较近;语义无关的词,向量距离较远。
- 上下文适应性:同一个词在不同语境下可能对应不同的向量表示(如多义词),从而承载更丰富的语义信息。
- 高维表征:为了捕捉复杂的语义关系,词向量通常是多维的(几十维到几百维),远高于简单的“向量化”所暗示的数学操作。
因此,词嵌入强调的是将离散的词语嵌入到连续的向量空间中,并保留其语义关联,而不仅仅是形式上的向量转换。
其实词嵌入的实现非常简单,通过将 token ID 对应的 One-Hot 向量乘以一个嵌入矩阵实现,如果词表的长度为 $N$,模型的维度为 $d_m$,则嵌入矩阵 $M_{\rm embedding} \in \mathbb{R}^{N \times d_m}$。
从这里可以看出,如果词表过大,那么 $M_{\rm embedding}$ 的维度也会增大,所以这样也会增加词嵌入过程的计算量;另外,如果词表过小,虽然会降低词嵌入过程的计算量,但同样长度的文本生成的 token 会更多,会增加下游训推任务的压力。
如果大家使用过 RAG 的话,会发现 RAG 中也有 Embedding 的概念,但 RAG 中的 Embedding 和上面讲解的 Embedding 是有些不同的。RAG 中的 Embedding 是对文本分块后得到的段落进行向量化处理,能够基于向量的内积计算相似度。RAG 中的 Embedding Model 通常也是基于 LLM 训练得到的。
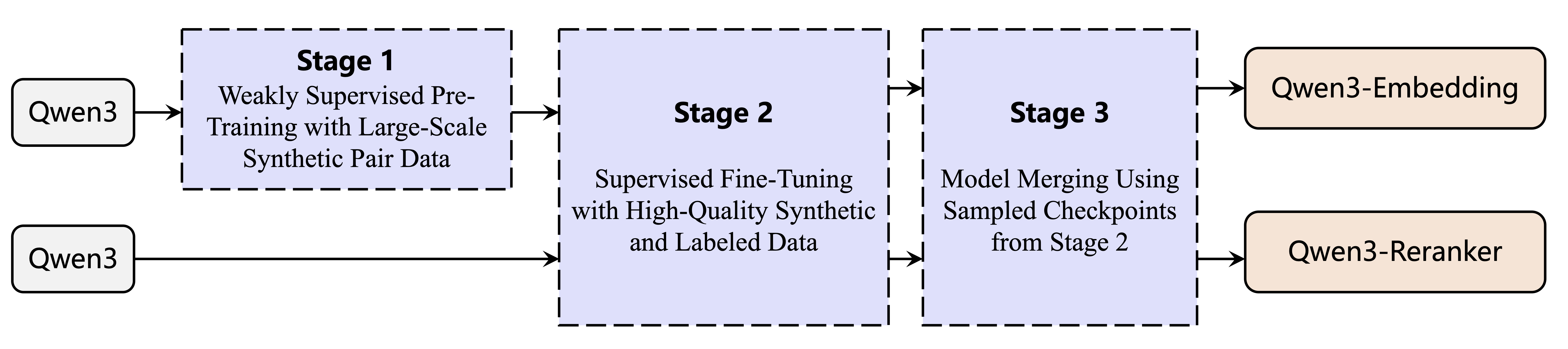
The Qwen3 embedding and reranking models are built on the dense version of Qwen3 foundation models and are available in three sizes: 0.6B, 4B, and 8B parameters. We initialize these models using the Qwen3 foundation models to leverage their capabilities in text modeling and instruction following.
3. Transformer 诞生的历史背景
《Attention Is All You Need》(Vaswani et al., 2017) 摘要:
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks that include an Encoder and a Decoder. The best performing models also connect the Encoder and Decoder through an attention mechanism.
翻译:
主流的序列转换模型基于复杂的递归或卷积神经网络,其中包括一个编码器和一个解码器。性能最好的模型还通过注意力机制将编码器和解码器连接起来。
3.1 Encoder-Decoder 架构
关键问题:
- 什么是 Encoder-Decoder 架构?
- 为什么主流的 Seq2Seq 模型都采用 Encoder-Decoder 架构?
在 Transformer 诞生的那个年代(2017 年),NLP 领域中主流的 Seq2Seq 模型都采用 Encoder-Decoder 架构。这种架构的设计理念并不难理解,可以表示为如下形式:
\[\begin{equation} \begin{aligned} H & = f_{\rm Encoder}(X) \\ \mathbf{y}_t & = f_{\rm Decoder}(H, [\mathbf{y}_1; \mathbf{y}_2; \dots ; \mathbf{y}_{t-1}]) \end{aligned} \end{equation}\]其中,$f_{\rm Encoder}(\cdot)$ 表示模型的 Encoder 模块,$X = [\mathbf{x}_1; \mathbf{x}_2; \dots ; \mathbf{x}_n]$ 表示模型的输入,$\mathbf{x}_i$ 为第 $i$ 个 token 的向量表示,$f_{\rm Encoder}(\cdot)$ 将输入 $X$ 转化为一种可被机器理解的隐藏(或中间)状态 $H$;$f_{\rm Decoder}(\cdot, \cdot)$ 表示模型的 Decoder 模块,$f_{\rm Decoder}(\cdot, \cdot)$ 基于 $H$ 自回归(Auto-Regressive)生成结果,$\mathbf{y}_i$ 表示生成的第 $i$ 个 token。
注:
自回归(Auto-Regressive,AR):是一种序列生成方法,其核心特征是:当前时刻的输出仅依赖于过去时刻的生成结果,并通过逐步迭代的方式构造完整序列。从概率建模的角度,这一过程可形式化表示为联合概率的链式分解 \(p(\mathbf{y}_{1:n}) = p(\mathbf{y}_1) \prod^n_{t = 2} p(\mathbf{y}_{t} \mid \mathbf{y}_{1:t-1})\)。
举个例子,当我们进行中英翻译时,通常会先通读整个中文句子,形成整体理解(即建立”语义表征”),然后基于这个理解逐步生成英文表达,这个认知过程恰好对应了 Encoder-Decoder 架构的工作机制:
- 编码阶段($f_{\rm Encoder}(\cdot)$):通过阅读理解源语句,将其抽象为包含关键语义信息的中间表征;
- 解码阶段($f_{\rm Decoder}(\cdot, \cdot)$):根据该语义表征,按目标语言规则逐步生成译文。
这种“先理解,再表达”的两阶段处理方式,正是现代机器翻译系统模仿人类翻译思维的核心设计。
对于 Encoder 与 Decoder,其实是按照功能对深度神经网络中的模块(或层)进行划分,通俗来讲,Encoder 负责将输入转化为机器可理解的某种表示(中间状态),Decoder 负责将这种表示转化为人类可理解的结果。
这里有个疑问,为什么有些模型无 Encoder 与 Decoder 一说?比如图像分类模型,以及什么样的模型适合使用 Encoder 与 Decoder?
深度神经网络可以视为一个非常复杂的函数,这个函数负责实现输入空间与输出空间之间的映射,当输出空间的结构较为简单或固定时,是无需特别在意 Encoder 与 Decoder 这些概念的,比如图像分类模型的输出仅仅是一个类型标签。但对于 Seq2Seq 模型,它的输出长度是不确定的,输出空间较为复杂,实现思路通常是先将输入序列转化为内部表示,在基于内部表示自回归生成结果,且在生成过程中需考虑输入序列与输出序列的不同位置间的依赖(或关联)程度。
3.2 注意力机制
在早期使用 RNN 或 CNN 构建的基于 Encoder-Decoder 架构的 Seq2Seq 模型中,自回归生成过程存在显著的上下文对齐局限性。具体表现为:解码器在生成目标序列的每一个 token 时,仅能隐式地依赖编码器输出的固定长度上下文表示(如 RNN 的最终隐藏状态或 CNN 的顶层特征),而无法显式建模当前生成位置与输入序列关键片段之间的动态关联关系。这种机制缺陷在 NLP 任务中会导致两类典型问题:
- 长距离依赖丢失,尤其是当输入序列较长时,编码器的信息压缩瓶颈会削弱关键输入的保留;
- 局部强相关忽略,例如在机器翻译任务中,生成目标语言动词时可能无法精准关联源语言中对应的谓语成分。
这一局限性的本质原因在于传统 Encoder-Decoder 架构的静态编码特性:编码阶段将变长输入序列压缩为固定维度的向量(Context Vector),而解码阶段缺乏对该向量的细粒度访问机制。直到注意力机制的引入,才通过计算 Decoder 的当前状态与 Encoder 的所有状态的动态权重解决了这一问题,这个过程也称为 Alignment Scores。
3.2.1 注意力机制的起源
注意力机制的雏形并非源自深度学习领域,其理论根源可追溯至 20 世纪 60 年代的统计学习框架——Nadaraya-Watson 核回归(1964)。该模型的数学表述为:
\[f(x) = \sum^n_{i=1} \alpha(x,x_i) y_i,\quad \alpha(x,x_i) = \frac{K(x - x_i)}{\sum^n_{j=1} K(x - x_j)}\]其中 $\alpha(x,x_i)$ 可视为一种原始形式的注意力权重。该模型通过核函数 $K(\cdot)$ 构建输入空间上的概率密度估计,给定查询值 $x$ 时,基于训练集 ${(x_i,y_i)}_{i=1}^n$ 计算条件期望 $E[y | x]$。具体而言:
- 相似度度量:核函数 $K(x-x_i)$ 本质是衡量查询 $x$ 与键 $x_i$ 的相似性度量,符合注意力机制中 Query-Key 匹配的核心思想;
- 权重归一化:通过 Softmax-Like 的分母项实现注意力权重的归一化($\sum_i\alpha(x,x_i)=1$);
- 上下文感知:输出是值 $y_i$ 的加权平均,权重随查询动态变化,这与现代注意力机制完全一致。
其实 Nadaraya-Watson 核回归和 KNN 算法也有些相似,可以看作是 KNN 算法的概率化表达。
3.2.2 注意力机制原理
注意力机制可视为 Nadaraya-Watson 核回归在神经网络中的推广形式,其核心创新在于:
- 将原始核权重 $\alpha$ 重构为 Softmax 归一化形式;
- 输入输出空间从标量推广到高维张量;
- 引入可学习的特征变换。
其通用数学表述为:
\[f(\mathbf{q}) = \sum^n_{i=1} \alpha(\mathbf{q}, \mathbf{k}_i)\mathbf{v}_i,\quad \alpha(\mathbf{q}, \mathbf{k}_i) = \mathrm{softmax}\left(K(\mathbf{q}, \mathbf{k}_i)\right)\]其中,$\mathbf{q} \in \mathbb{R}^d$ 为查询向量(Query),$\mathbf{k}_i \in \mathbb{R}^d$ 为键向量(Key),$\mathbf{v}_i \in \mathbb{R}^m$ 为值向量(Value),$K(\cdot,\cdot)$ 为注意力评分函数。
注:${\rm softmax}$ 是一种在机器学习中广泛使用的算子,对于向量 $\mathbf{x} = [x_1, x_2, \dots ,x_n]$,${\rm softmax}_i(\mathbf{x}) = \frac{e^{x_i}}{\sum^n_{k=1}e^{x_k}}$,它可以将 $\mathbf{x}$ 中的每个元素转化为一个 $0$ 至 $1$ 间的值,且所有元素转化后的值和为 $1$。
现代注意力机制主要采用两种评分函数:
- 加性注意力(Additive Attention):$K(\mathbf{q}, \mathbf{k}) = \mathbf{w}^T \sigma(\mathbf{W}_q\mathbf{q} + \mathbf{W}_k\mathbf{k})$
- 优点:通过全连接层实现跨维度交互,激活函数 $\sigma$(通常为 $\tanh$)提供非线性表达能力;
- 缺点:参数量大,计算复杂度高。
- 缩放点积注意力(Scaled Dot-Product Attention):$K(\mathbf{q}, \mathbf{k}) = \mathbf{q}^T\mathbf{k} / \sqrt{d}$
- 优点:计算高效,无需额外参数;
- 关键改进:使用缩放因子 $\sqrt{d}$ 防止高维点积值过大导致梯度消失。
发展趋势:
- 加性注意力在早期 Seq2Seq 模型中表现优异;
- 缩放点积注意力因计算效率成为 Transformer 架构的标准配置;
- 大语言模型普遍采用多头缩放点积注意力,通过并行计算实现高效处理长序列。
3.3 Transformer 解决的问题
当时主流的序列转换模型是基于 Encoder-Decoder 架构的 RNN 或 CNN。RNN 无法较好地实现并行化;CNN 无法较好地计算输入序列与输出序列的不同位置间的依赖程度,距离越远所需的计算量越大。
Transformer 主要想达到这两个目标:
- 能够较好地支持并行化;
- 能够很方便地计算输入序列与输出序列的不同位置间的依赖程度的。
4. Transformer 工作原理
Transformer 是一个完全基于注意力机制的 Seq2Seq 模型,其核心创新在于完全摒弃了 RNN 与 CNN,仅依靠自注意力机制和前馈神经网络(Feed Forward Network)构建编码器-解码器结构。这一突破性设计使得 Transformer 能够高效地建模长距离依赖关系,并实现并行化计算。正因如此,其论文的标题才命名为”Attention Is All You Need”。
图 4 展示了 Transformer 的整体架构,通过前文的铺垫,大家或许已对 Transformer 的架构设计有了一定感触。
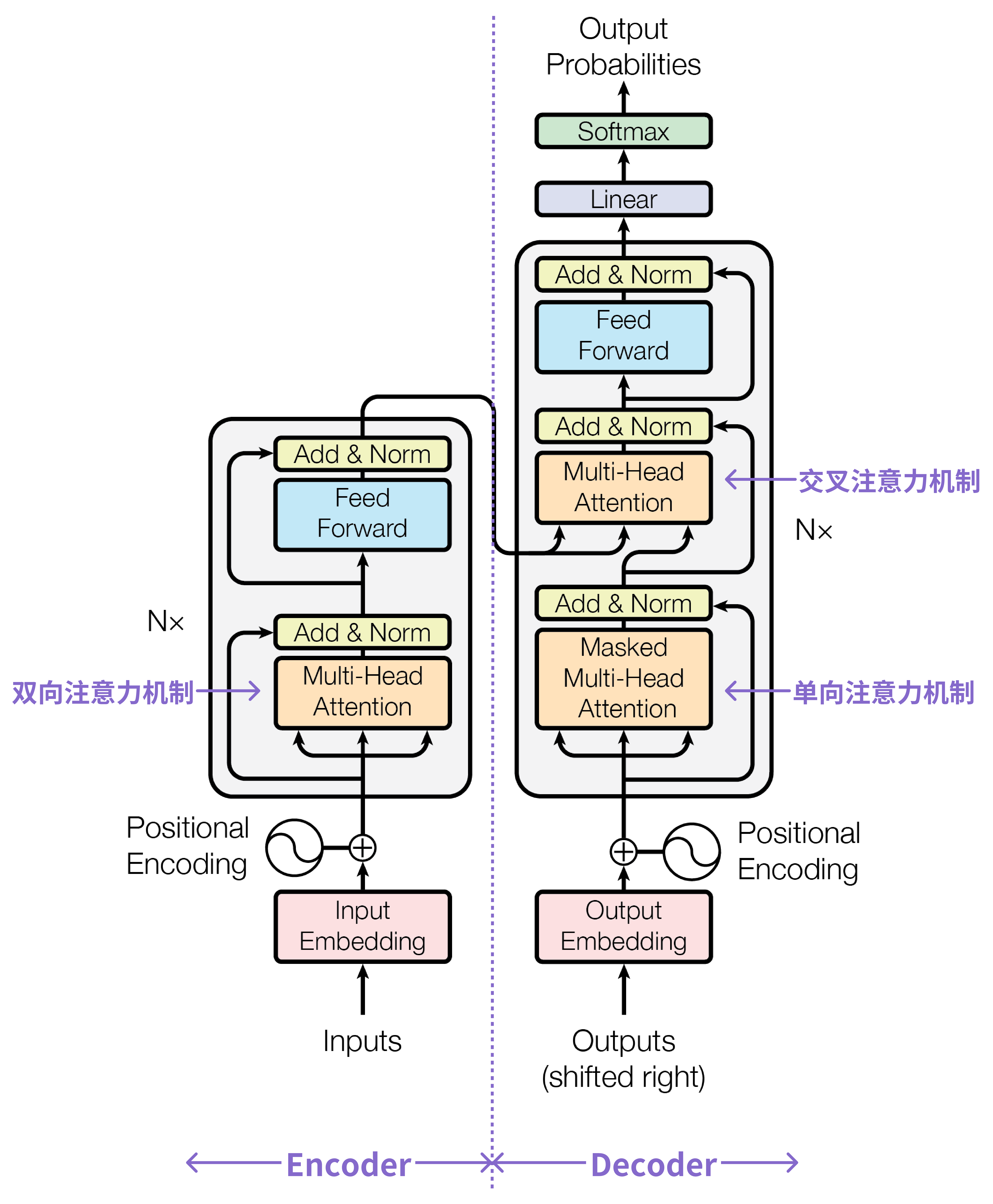
接下来我们按 Transformer 模型的主要模块来介绍,主要有多头注意力机制、位置编码、前馈神经网络与 Add & Norm 这几个核心模块。
4.1 多头注意力机制
在深度学习中,“头”可以理解为独立、并行的计算单元。
Transformer 采用了多头注意力机制(Multi-Head Attention,MHA)而不是传统的注意力机制以增强模型的表达能力这种,机制可以理解为:
- 并行计算:将输入序列通过多个独立、并行的注意力机制算子(或注意力头)同时进行计算处理;
- 模式学习:每个注意力头学习不同的注意力模式,例如,有的注意力头擅长捕捉长距离依赖关系,有的关注局部语法特征,有的提取特定语义信息等;
- 特征融合:最后将所有注意力头的输出拼接,并通过线性变换得到最终结果。
下面举几个例子来做一些辅助说明:
- 长距离依赖关系,比如“The cat that wandered into our garden last winter was starving, but now is happily napping in the sun.”这段英文叙述,第 10 个词为“was”而不是“were”取决于第 2 个词“cat”。
- 局部语法特征,比如“a book”与“an apple”,根据名词的发音特征,前者使用“a”,后者使用“an”。
- 特定语义,比如“我的车旁边停了一辆剁椒鱼头”与“这家店的剁椒鱼头还不错”,两者中的“剁椒鱼头”语义是不同的。
这种架构设计使得模型能够从不同的角度协同学习多样化的特征表示,从而更全面地建模序列内部的复杂关系。
前文有提及,对于将输入序列构建为内在表示(理解)与基于内在表示自回归生成结果(表达)两个过程,Transformer 皆使用注意力机制完成,而非传统的 RNN 与 CNN。 因为用于注意力机制(详见 3.2 小节)计算的 query、key、value 完全由输入 token 序列通过线性变换(乘以一个矩阵,这个矩阵是需要学习的参数)而来,所以这种设计模式被称为自注意力机制。
下面简单介绍一下计算过程,假设 $\mathbf{t}_i$ 表示第 $i$ 个 token(Embedding 表示),$j$ 表示第 $j$ 个注意力头,$\mathbf{t}_i$ 在第 $j$ 个注意力头中的 query、key 与 value 分别表示为 $\mathbf{q}_{i, j}$、$\mathbf{k}_{i, j}$ 与 $\mathbf{v}_{i, j}$。
首先,按头对输入的每个 token $\mathbf{t}_i$ 进行线性变换,得到对应的 query、key 与 value:
\[\mathbf{q}_{i, j} = W^Q_j \mathbf{t}_i\] \[\mathbf{k}_{i, j} = W^K_j \mathbf{t}_i\] \[\mathbf{v}_{i, j} = W^V_j \mathbf{t}_i\]其中,$t_i \in \mathbb{R}^{d_{\rm model}}$,$W^Q_j \in \mathbb{R}^{d_k \times d_{\rm model}}$,$W^K_j \in \mathbb{R}^{d_k \times d_{\rm model}}$,$W^V_j \in \mathbb{R}^{d_v \times d_{\rm model}}$,在大多数情况下 $d_k = d_v = d_{\rm model}/n_h$,$d_{\rm model}$ 为模型的维度,$n_h$ 为头的总数。
然后,在每个头上计算缩放点积注意力:
\[\mathbf{o}_{i, j} = \sum^n_{k=1} {\rm softmax}_k \left(\frac{\mathbf{q}_{i, j}^T \mathbf{k}_{k, j}}{\sqrt{d}} \right) \cdot \mathbf{v}_{k, j} = \sum^n_{k=1} \frac{\frac{e^{\mathbf{q}_{i, j}^T \mathbf{k}_{k, j}}}{\sqrt{d}}}{\sum^n_{m=1}\frac{e^{\mathbf{q}_{i, j}^T \mathbf{k}_{m, j}}}{\sqrt{d}}} \cdot \mathbf{v}_{k, j}\]其中,$n$ 为每个 batch 中 token 的数量。可以看出,对于第 $j$ 个头,其输出 $\mathbf{o}_{i, j}$ 为 $[\mathbf{v}_{1,j}, \mathbf{v}_{2,j},\dots,\mathbf{v}_{n,j}]$ 的线性组合,可以简写为 $\mathbf{o}_{i, j} = \sum^n_{k=1} \alpha_k \mathbf{v}_{k,j}$,在机器学习中通常用向量的内积来衡量两个向量的相似度,$\mathbf{q}_{i, j}$ 与 $\mathbf{k}_{k, j}$ 的内积越大,或 $\mathbf{q}_{i, j}$ 与 $\mathbf{k}_{k, j}$ 越相似,$\mathbf{v}_{k,j}$ 的权重 $\alpha_k$ 就会越大,$\mathbf{v}_{k,j}$ 所占的比重就会越大。简单来讲就是,与当前的词越相近的词,对结果的影响越大。
最后,将所有头的输出拼接并通过线性变换:
\[\mathbf{u}_i = W^O[\mathbf{o}_{i, 1}; \mathbf{o}_{i, 2} ; \dots ; \mathbf{o}_{i, n_h}]\]从图 4 可以看出,在 Transformer 中共有 3 个地方用到了多头注意力机制,第 1 个地方在 Encoder 模块,第 2、3 个地方在 Decoder 模块。 Encoder 中的多头注意力机制为普通的多头注意力机制(也称为双向注意力机制), Decoder 下方的多头注意力机制(即 Masked Multi-Head Attention)为单向注意力机制(也称为因果注意力机制),Decoder 上方的多头注意力机制为交叉注意力机制。
这三种多头注意力机制的计算框架和上述是类似的,但有一些细微的差别。
4.1.1 双向注意力机制
Encoder-Decoder 架构的核心思想是“先理解后生成”。其中 Encoder 的核心任务是实现对输入的深度理解,这一过程通过全序列扫描实现。具体表现为:当处理长度为 $l$ 的输入序列 $X = [\mathbf{t}_1, \mathbf{t}_2, \dots, \mathbf{t}_l]$ 时,每个位置的注意力计算会同时考虑序列中所有 token 的 key-value 对。因此公式(11)中的求和上限应修正为序列长度 $l$:
\[\mathbf{o}_{i, j} = \sum^{\color{red} l}_{k=1} {\rm softmax}_k \left(\frac{\mathbf{q}_{i, j}^T \mathbf{k}_{k, j}}{\sqrt{d}} \right) \cdot \mathbf{v}_{k, j}\]这种全局可见的注意力模式使 Encoder 能够建立完整的上下文表征。
4.1.2 单向注意力机制
Decoder 负责基于 Encoder 生成的中间表示自回归生成结果,对于自回归过程,当前的输出只取决于之前的结果,与未来的结果无关。
训练阶段
对于训练数据,Decoder 只能看到当前位置以及之前位置的信息,不能看到后续位置的信息,Decoder 采用因果掩码(Causal Mask),确保第 $i$ 个位置的 query 只能访问前 $i$ 个位置的 key-value 信息,因果掩码 $M \in \mathbb{R}^{n \times n}$ 通常为一个下三角矩阵(元素为 $1$ 或 $0$),可以写为如下形式:
因果掩码使得 Softmax 算子在计算当前 query 与未来位置的 key 的内积时会得到 $0$,
\[\mathbf{o}_{i, j} = \sum^{\color{red} l}_{k=1} {\rm softmax}_k\left( M_{i,k} \cdot \frac{\mathbf{q}_{i, j}^T \mathbf{k}_{k, j}}{\sqrt{d}}\right) \cdot \mathbf{v}_{k, j}\]推理阶段
由于解码是逐步进行的,不断基于历史状态生成下一个 token,模型只需计算当前 query 相对于当前及历史 key-value 对的注意力,无需掩码。为提升效率,通常会缓存历史 key-value 对,避免重复计算历史 token 与 $W^K$、$W^V$ 的乘积。
4.1.3 交叉注意力机制
在解码阶段,Decoder 需要将 Encoder 输出的上下文表征(通常记为 $\mathbf{U} = [\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_n]$)融入生成过程。交叉注意力机制的查询(query)来自 Decoder 的当前状态,而 key-value 对则来自 Encoder 的最终输出:
\[\mathbf{o}_{i, j} = \sum^{\color{red} l}_{k=1} {\rm softmax}_k \left(\frac{\mathbf{q}_{i, j}^T {\mathbf{\color{red} u}_{\color{red} k}}}{\sqrt{d}} \right) \cdot \mathbf{\color{red} u}_{\color{red} k}\]该机制实现了 Encoder-Decoder 之间的信息桥接,是序列到序列建模的关键组件,这种设计使得模型能够同时关注不同位置的表示子空间,学习更丰富的上下文依赖关系,提高模型的泛化能力。
在多模态大模型中,通常也是基于交叉注意力机制对齐不同模态间的语义。
4.2 位置编码
自注意力机制本身具有置换(轮换)不变性(Permutation Invariance),在注意力机制中,当前的 query 与某一个 key-value 对的计算结果与当前 key-value 对在序列中的位置是无关的,这意味着模型无法识别输入序列的位置信息,为了保留关键的位置信息,Transformer 引入了位置编码机制。
注:
Permutation Invariance is a property of a mathematical function or algorithm that remains unchanged even when the order of its inputs is altered.
这个设计基于这样一种想法,同样的一个词对,它们距离得越近,相关程度应该越大,比如,一本书中的某个词对,它们在同一页中的相关程度要比在不同章节中的相关程度要大。
位置编码主要实现两个目标:
- 打破置换不变性;
- 能够表达相对位置信息,并具有远程衰减性质。
该机制通过将词嵌入向量与位置编码信息相加来实现,原始 Transformer 论文中使用的位置编码被称为 Sinusoidal 位置编码,实现如下公式所示:
\[\begin{equation} \begin{aligned} PE_{(pos, 2i)} & = \sin(pos / 10000^{2i/d_{\rm model}}) \\ PE_{(pos, 2i+1)} & = \cos(pos / 10000^{2i/d_{\rm model}}) \end{aligned} \end{equation}\]其中,$pos$ 表示当前 token 在序列中的位置,$i$ 表示 token 的维度特征。
Transformer 原始论文中并未具体说明为什么要这样设计,如果想深入了解,可以阅读 (苏剑林, 2021),里面的数学推导有一些复杂,从中可以看出这个设计需要满足一定限制才能实现上述目标,比如 PE 不能过大。
还有很多其他的位置编码技术,目前比较火的是旋转位置编码(Rotary Position Embedding,RoPE)(Su et al., 2023),在 DeepSeek 系列模型中有广泛使用,它的设计其实非常简单,如下公式所示:
\[\begin{equation} \begin{aligned} \mathbf{q}^{\rm rope}_i &= \mathcal{R}(i \theta) \mathbf{q}_i \\ \mathbf{k}^{\rm rope}_j &= \mathcal{R}(j \theta) \mathbf{k}_j \\ \left \langle \mathbf{q}^{\rm rope}_i, \mathbf{k}^{\rm rope}_j \right \rangle &= \mathbf{q}_i^T \mathcal{R}(i \theta)^T \mathcal{R}(j \theta) \mathbf{k}_j = \mathbf{q}_i^T \mathcal{R}(-i \theta) \mathcal{R}(j \theta) \mathbf{k}_j = \mathbf{q}_i^T \mathcal{R}((j-i) \theta) \mathbf{k}_j \end{aligned} \end{equation}\]其中,$q_i$ 为第 $i$ 个 token 对应的 query,$k_j$ 为第 $j$ 个 token 对应的 key,$\mathcal{R}(m \theta)$ 为对应的旋转矩阵。想要详细了解 RoPE 可以看看这个视频(旋转位置编码 RoPE 的简单理解)。
4.3 Add & Norm
Transformer 架构对每个子层(自注意力层、前馈网络层)都采用了 Add & Norm,即每个子层的输出为 ${\rm LayerNorm(x + {\rm SubLayer}(x))}$,其中,${\rm SubLayer}(\cdot)$ 为当前子层的实现,${\rm LayerNorm}$ 为层归一化。
4.3.1 残差连接
这一小节主要参考 DIVE INTO DEEP LEARNING 7.6 小节
残差连接(Residual Connection)最早源于 (He et al., 2015) ,用于构建图像识别的深层神经网络,这个设计对如何构建深层神经网络产生了深远的影响。残差连接的核心理念是每个附加层都应该更容易地包含原始函数作为其元素之一。
这种设计有两个好处:
- 表达能力:能够保证新函数可以包含原始函数,两者具有嵌套关系,即神经网络的下一层的表达能力一定不会比上一层弱;
- 数值稳定性:由于上一层的结果可以直接传递到下一层的输出中,能够有效缓解深层网络的梯度消失问题。
4.3.2 层归一化
层归一化(Layer Normalization)(Ba et al., 2016) 是沿特征维度对输入进行归一化,假设向量 $\mathbf{x} \in \mathbb{R}^d$,$\mathbf{x}_i$ 表示 $\mathbf{x}$ 的第 $i$ 个元素,$\mathbf{x}$ 的层归一化结果如下所示:
\[\begin{equation} \begin{aligned} \hat{\mathbf{x}}_i &= \beta \frac{\mathbf{x}_i - \mu}{\sqrt{\sigma^2 + \epsilon}} +\gamma \\ \mu &= \frac{1}{d} \sum^d_{i=1} \mathbf{x}_i \\ \sigma^2 &= \frac{1}{d} \sum^d_{i=1} (\mathbf{x}_i - \mu)^2 \end{aligned} \end{equation}\]其中,$\epsilon$ 是一个很小的常量,避免分母为 0,保证数值稳定,$\beta$、$\gamma$ 是可学习的参数。
层归一化的作用主要有两点:
- 稳定各层的输入分布,保证数值稳定性,避免梯度爆炸或消失;
- 加速模型收敛。
另外,计算机视觉(CV)中常采用批归一化(BatchNorm),即沿批次维度归一化,而 NLP 中偏好层归一化,这种差异主要源于文本数据的变长特性与批处理挑战。
4.4 基于位置的前馈网络
基于位置的前馈网络(Position-wise Feed-Forward Networks)是一个使用 ReLU 激活函数连接起来的两层全连接层,可以写为如下形式:
\[{\rm FFN}(x) = \max(0,x W_1 + b_1) W_2 + b_2\]至于为什么叫做基于位置的前馈网络?模型各层间的输入与输出的尺寸为 $(b, n, d)$,$b$ 表示 Batch Size,$n$ 表示序列的长度,$d$ 表示模型的维度,在输入抵达 FFN 时,会将输入的尺寸从 $(b, n, d)$ 转化为 $(bn, d)$,然后 FFN 对输入逐行进行计算,上述公式中的 $x$ 表示输入的每一行,基于位置的含义就体现在这里,计算完成后,再将输出的尺寸从 $(bn, d)$ 转化为 $(b, n, d)$。
至于为什么要使用 FFN,只有注意力机制不行吗?FFN 主要有以下作用:
- 引入非线性变换:自注意力机制本质上是一个线性加权求和的过程,FFN 中的激活函数能够为模型引入非线性能力,避免层数塌陷。
- 对信息进行深度加工和转换:自注意力机制负责处理全局信息,而 FFN 则逐 token 进行计算,提炼出更深层的内在表示。一个常见的比喻是,自注意力机制负责 “沟通” ,让每个词了解其他词在说什么;FFN 负责 “思考” ,让每个词基于沟通得到的信息,自己进行深入的计算和内化。
FFN 能够提供一种知识存储的机制。有研究认为,FFN 的两层线性层扮演了“键值记忆”的角色。其中第一个线性层($W_1$)充当“键”,用于匹配特定的信息模式,而第二个线性层($W_2$)则输出对应的“值”,即存储的知识或反应。当输入向量的模式与 FFN 学习到的某个“键”匹配时,它就会触发并输出相应的知识。这使得 FFN 层可以存储大量的、独立于上下文的事实知识(Factual Knowledge)。
FFN 能够维持维度稳定性并增加模型容量。FFN 通常先放大维度再缩小回来。这个“瓶颈”结构既能增加模型的参数数量和容量(使其能够学习更复杂的东西),又能保证输入和输出的维度一致,从而可以轻松地堆叠多个 Transformer 块。
在目前的 LLM 中,大部分参数都集中在 FFN 层中。对于 FFN 层的设计,目前主要有两种架构,一种是 MoE(Mixture of Expert,混合专家)架构,一种是 Dense 架构。
Dense 架构就是上文讲解的 Transformer FFN 层的架构设计。在 Dense 架构中,每一个输入 token 都会激活整个网络的所有参数。也就是说,对于模型处理的每一个字或词,整个庞大的神经网络都会参与计算,给出输出。模型越大(参数越多),计算量(FLOPS)和内存占用就越高,推理速度也越慢。
Dense 架构的优势主要有两点:
- 由于所有参数都参与每次计算,模型可以学习到非常复杂和通用的表征,模型的理解表达能力更强。
- 架构统一,易于实现,训练和推理逻辑简单。
Dense 架构的缺点也很明显,扩展昂贵,要想提升模型能力,最直接的方式就是增加参数量(比如从百亿到千亿、万亿)。但这会导致计算成本、显存占用和能耗呈平方级甚至更快的增长,使得万亿参数级别的 Dense 模型在推理时几乎不现实。
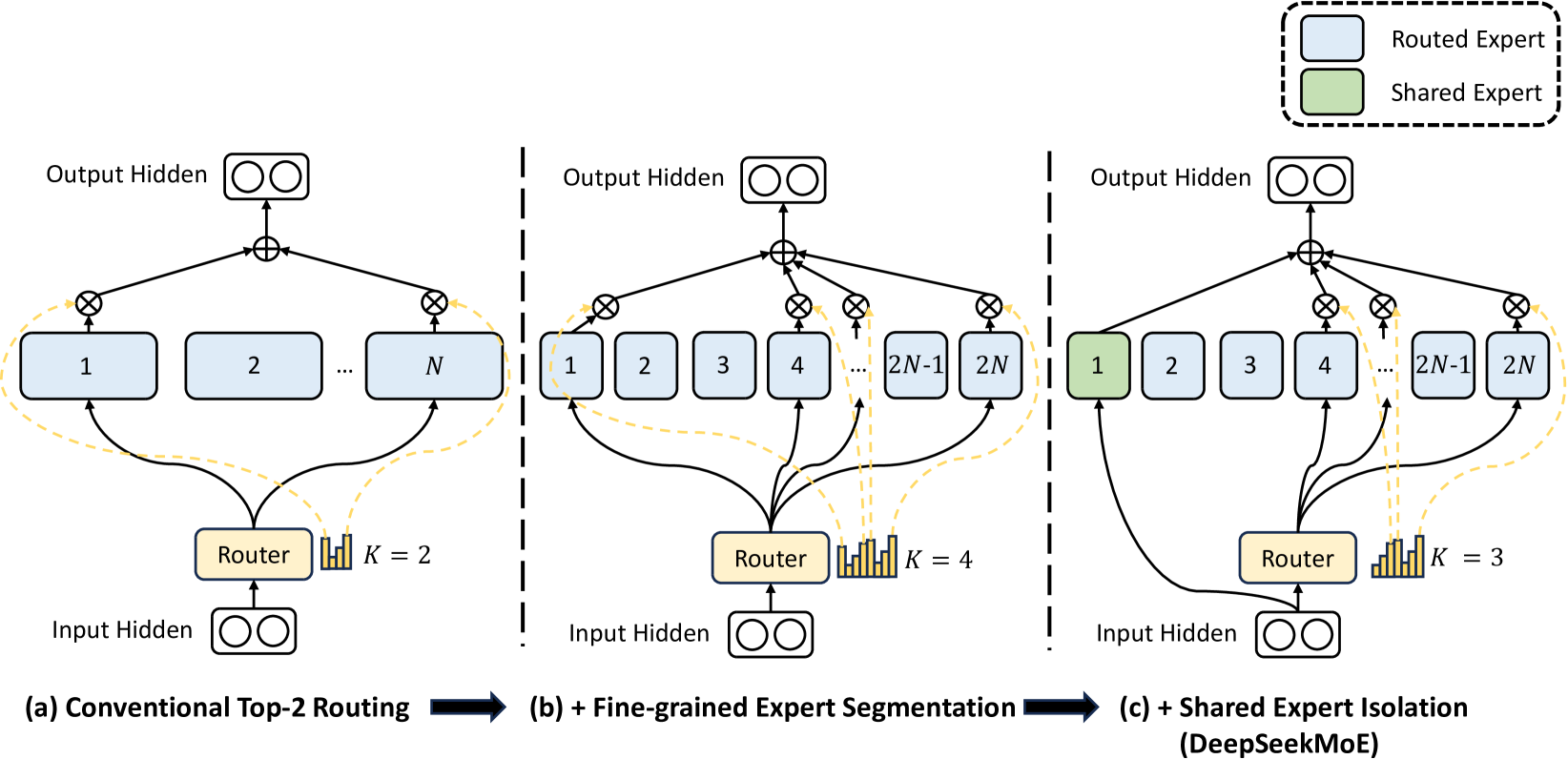
MoE 架构是为了解决 Dense 模型扩展性瓶颈而诞生的。它的核心思想是 “分而治之”。一个 MoE 层由多个“专家”组成,每个专家本身是一个小型神经网络(例如一个小型 FFN)。同时,有一个关键的“门控网络”或“路由网络”。
MoE 层的工作流程如下:
- 对于一个输入 token,门控网络会计算它应该被分配给哪个或哪几个“专家”。
- 只有被选中的专家才会被激活并对这个 token 进行计算。
- 最后,将各个专家输出的结果根据门控网络的权重进行加权合并,作为最终的输出。
在 MoE 模型中,能够做到有万亿参数,但处理每个 token 时可能只激活其中的几十亿或百亿参数。另外,路由算法至关重要,MoE 算法需要高效、准确地将 token 分配给最合适的专家,糟糕的路由会导致负载不均衡或性能下降,所以 MoE 模型的训练难度会远高于 Dense 模型。
5. 关于 LLM 的闲谈
对于现代大模型,有一种趋势,模型或算法可能越来越趋向于简单,通过增大数据与模型的规模(涌现能力)来弥补模型或算法的简单,也可以说只有简单的结构才容易扩大规模,尺寸做得更大更深。但这对 AI 的 Infra、分布式训练等的要求也变得更高。
回顾 DeepSeek 这一年的更新 (zartbot, 2025),一直在优化内存与 I/O,混合精度降低模型的内存占用,MoE 降低 FFN 层激活的参数数量,MLA 降低 KV Cache,再到 NSA 与 DSA 降低 Attention 本身的计算。
之前在知乎上看到一个很火的问题,为什么现在 LLM 普遍使用 Decoder-Only 架构?对于同质的结构,模型更容易做得更大更深,而 Encoder 更善于理解,Decoder 更善于生成。早期大语言模型分为 Encoder-Only 架构与 Decoder-Only 架构两个流派,Encoder-Only 架构以 Google 的 Bert 模型为代表,Decoder-Only 架构以 OpenAI 的 GPT 系列模型为代表。当时 Bert 的性能是要优于 GPT 的,后来由于数据与模型规模的增大及涌现能力的出现,GPT 的性能超越了 Bert。Encoder-Only 模型的训练要比 Decoder-Only 模型更复杂,我的理解是,在早期数据与模型规模没有那么大的时候,复杂模型相对于简单模型是有优势的,但随着数据与模型的规模不断增加,这种优势会慢慢减弱。另外 Encoder 的双向注意力机制存在低秩问题 (苏剑林, 2023),这可能会削弱模型的表达能力,在这一点上 Decoder-Only 模型也更有优势。
在 LLM 中,还有一个经常出现的概念,PD 分离,PD 分离是指将推理时的 Prefill 和 Decode 两个阶段放在不同的机器中处理,Prefill 阶段更侧重于并行,Decode 阶段更侧重于串行和内存访问。
参考文献
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention Is All You Need. CoRR, abs/1706.03762. http://arxiv.org/abs/1706.03762
- Wu, Y., Schuster, M., Chen, Z., Le, Q. V., Norouzi, M., Macherey, W., Krikun, M., Cao, Y., Gao, Q., Macherey, K., Klingner, J., Shah, A., Johnson, M., Liu, X., Kaiser, Ł., Gouws, S., Kato, Y., Kudo, T., Kazawa, H., … Dean, J. (2016). Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation. https://arxiv.org/abs/1609.08144
- Shibata, Y., Kida, T., Fukamachi, S., Takeda, M., Shinohara, A., Shinohara, T., & Arikawa, S. (1999). Byte pair encoding: A text compression scheme that accelerates pattern matching.
- Kudo, T. (2018). Subword Regularization: Improving Neural Network Translation Models with Multiple Subword Candidates. https://arxiv.org/abs/1804.10959
- Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient Estimation of Word Representations in Vector Space. https://arxiv.org/abs/1301.3781
- 苏剑林. (2021). Transformer升级之路:1、Sinusoidal位置编码追根溯源. https://kexue.fm/archives/8231
- Su, J., Lu, Y., Pan, S., Murtadha, A., Wen, B., & Liu, Y. (2023). RoFormer: Enhanced Transformer with Rotary Position Embedding. https://arxiv.org/abs/2104.09864
- He, K., Zhang, X., Ren, S., & Sun, J. (2015). Deep Residual Learning for Image Recognition. https://arxiv.org/abs/1512.03385
- Ba, J. L., Kiros, J. R., & Hinton, G. E. (2016). Layer Normalization. https://arxiv.org/abs/1607.06450
- Dai, D., Deng, C., Zhao, C., Xu, R. X., Gao, H., Chen, D., Li, J., Zeng, W., Yu, X., Wu, Y., Xie, Z., Li, Y. K., Huang, P., Luo, F., Ruan, C., Sui, Z., & Liang, W. (2024). DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models. https://arxiv.org/abs/2401.06066
- Zhang, Y., Li, M., Long, D., Zhang, X., Lin, H., Yang, B., Xie, P., Yang, A., Liu, D., Lin, J., Huang, F., & Zhou, J. (2025). Qwen3 Embedding: Advancing Text Embedding and Reranking Through Foundation Models. https://arxiv.org/abs/2506.05176
- zartbot. (2025). 学习一下DeepSeek-V3.2. https://mp.weixin.qq.com/s/LYhfpduM72hEJJGe2GFDXw
- 苏剑林. (2023). 为什么现在的LLM都是Decoder-only的架构?. \urlhttps://kexue.fm/archives/9529
- Tie, G., Zhao, Z., Song, D., Wei, F., Zhou, R., Dai, Y., Yin, W., Yang, Z., Yan, J., Su, Y., Dai, Z., Xie, Y., Cao, Y., Sun, L., Zhou, P., He, L., Chen, H., Zhang, Y., Wen, Q., … Gao, J. (2025). A Survey on Post-training of Large Language Models. https://arxiv.org/abs/2503.06072